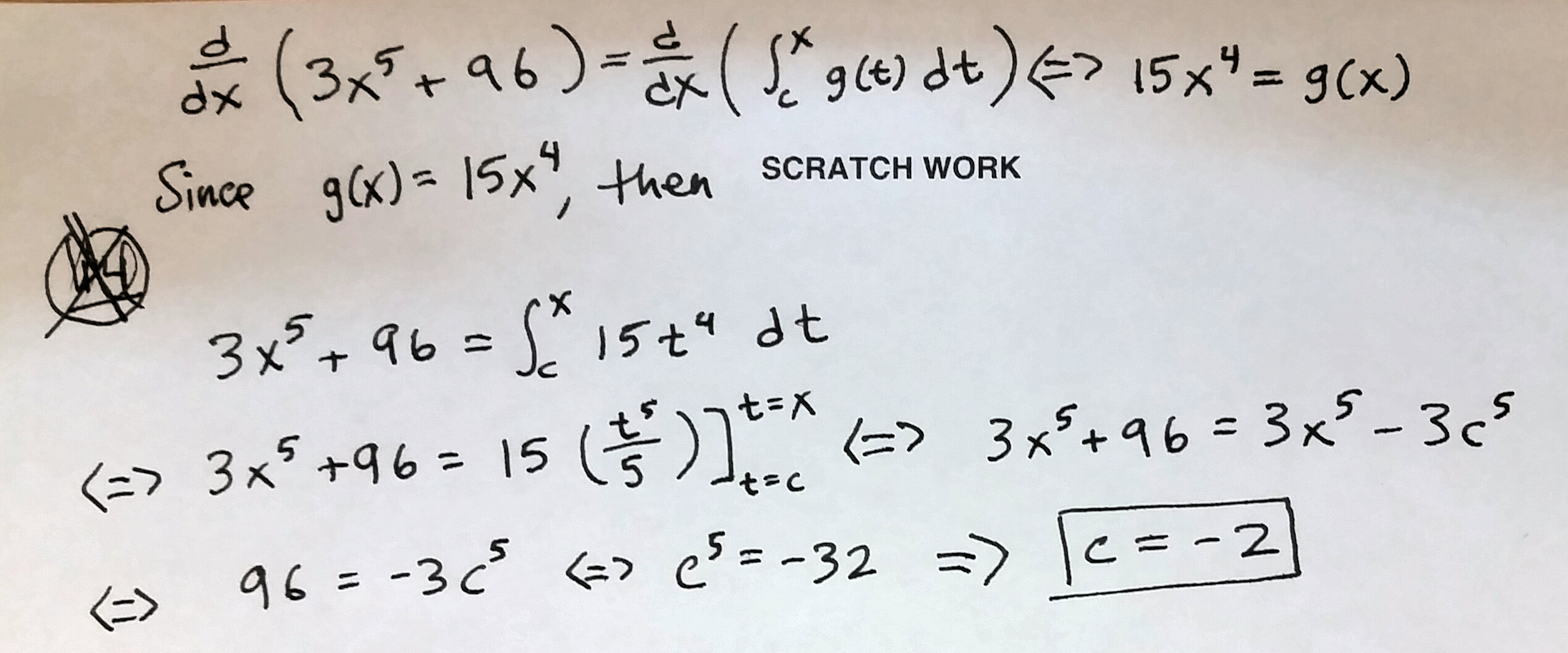
Studying for the exam I've encountered two problems. The first is stated as follows:

If \(f\) is a continuously differentiable real-valued function defined on the open interval \((-1,4)\) such that \(f(3)=5\) and \(f'(x)\geq-1\) for all \(x\), what's the greatest value of \(f(0)\)?

The second I thought was difficult too and worth sharing:

Suppose \(g\) is a continuous real-valued function such that \(3x^5+96=\int_c^x g(t) dt\) for each \(x \in \mathbb{R}\), where \(c\) is a constant. What is the value of \(c\)?

What approach do you have to answer the two problems?