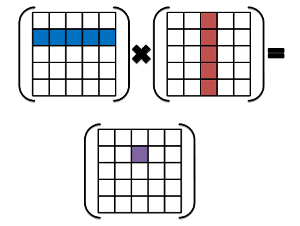
How should we best understand matrix multiplication? In other words, what concepts motivate us to define the operation of multiplying two matrices?

Let's begin with the concepts. First, we must know what are linear maps on finite vector spaces. Then given a vector space, we must understand the idea of its basis and dimension. So let \(V\) and \(W\) be vector spaces and \(T: V \rightarrow W\) be a linear map such that \(V\) fiinite. In the beginning of our journey we discover that the sets $$ \text{null }T = \{ v \in V: T(v) = 0 \} \wedge \text{range }T = \{w \in W: (\exists v \in V)\text{ }T(v) = w \}$$ are subspaces of \(V, W\). We then relate these subspaces and their dimension with the important equality that $$\dim{V} = \dim{\text{null }T} + \dim{\text{range }T}.$$ Sheldon Axler names the above equation the "Fundamental Theorem of Linear Maps". Using this formula allows us to conclude and discover many facts about the subject.

We then discover that a linear map is uniquely determined from the mapping of basis elements of \(V\) to elements in \(W\). This information of the linear map is then succinctly described and organized in associating it with a unique matrix named the matrix of the linear map. Let us denote it by \(\mathcal{M}(T)\). Before we attempt to define matrix multiplication, recall that the composition of two linear maps is a linear map when the composition makes sense.

We now begin our calculated definition of what it means to multiply two matrices. Let \(S \in \mathcal{L}(V,W), T \in \mathcal{L}(U,V)\) and \(ST \in \mathcal{L}(U,W) \) where \( \{v_1, \ldots, v_n\}, \{w_1,\ldots,w_m\},\text{ and, } \{u_1, \ldots, u_p\}\) are bases of \(V,W,\) and \(U\). Here we denote the set of all linear maps from \(V\) into \(W\) as \(\mathcal{L}(V,W)\). We want \( \mathcal{M}(ST) = \mathcal{M}(S) \times \mathcal{M}(T)\) to make sense. To that end, denote \(\mathcal{M}(S), \mathcal{M}(T),\) and \(\mathcal{M}(ST)\) by \(A,C\) and \(AC\). We then have in symbols that \(A,C\) and \(AC\) are equal to $$ \begin{array}{cc}

\begin{array}{c c} & \begin{array} {@{} c c c @{}} v_1 & \cdots & v_n \end{array} \\ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array}\hspace{-1em} & \left( \begin{array}{@{} c c c @{}} A_{11} & \cdots & A_{1n} \\ \vdots & & \vdots \\ A_{m1} & \cdots & A_{mn} \end{array} \right) \\ \end{array} & \begin{array}{c c} & \begin{array} {@{} c c c @{}} u_1 & \cdots & u_p \end{array} \\ \begin{array}{c} v_1 \\ \vdots \\ v_n \end{array}\hspace{-1em} & \left( \begin{array}{@{} c c c @{}} C_{11} & \cdots & C_{1p} \\ \vdots & & \vdots \\ C_{n1} & \cdots & C_{np} \end{array} \right) \\ \end{array} \\[2em]

\begin{array}{c c} & \begin{array} {@{} c c c @{}} u_1 & \cdots & u_p \end{array} \\ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array}\hspace{-1em} & \left( \begin{array}{@{} c c c @{}} (AC)_{11} & \cdots & (AC)_{1p} \\ \vdots & & \vdots \\ (AC)_{m1} & \cdots & (AC)_{mp} \end{array} \right) \end{array}. \end{array} $$

We then have for \(1 \leq k \leq p \) that $$ \begin{align} (ST)u_k &= S(Tu_k) \\ &= S(\sum_{r=1}^{n}C_{r,k}v_r) \\ &= \sum_{r=1}^{n}C_{r,k}Sv_r \\ &= \sum_{r=1}^{n}C_{r,k}\sum_{j=1}^{m}A_{j,r}w_j \\ &= \sum_{j=1}^{m}\sum_{r=1}^{n}A_{j,r}C_{r,k}w_j. \end{align} $$

From the above calculation, we see that for \(1 \leq j \leq m\) we have that \( (AC)_{j,k} = \sum_{r=1}^{n}A_{j,r} C_{r,k} \), and it is this formula we use as our working definition of matrix multiplication.